Introduction
Velocity is relative. When one states: "I am moving at a rate of 2 meters per second", one actually assumes that there is some reference point, relative to which he is changing the distance. In exactly the same way, when an astronomer states: "this gas cloud is rotating around the galactic center at a rate of 80 Km/sec", she actually means that she has been supplied with a well defined frame of reference, relative to which this value is valid. The observed values presented in rotation curves are also valid only with respect to some specific frame of reference. The only question is whether this frame is an Inertial one.
Why is it relevant? Because currently, when fitting rotation curves, astrophysicists take this quality for granted. Modeling a rotation curve (from the corresponding mass distribution) implicitly relies on this assumption. We shall come back to this point later, but first let's define what an Inertial frame is.
Inertial Frames
Strictly speaking, an Inertial frame is a frame of reference relative to which the Law of Inertia holds. The law of Inertia (i.e. the first law of Newton) states that an object either remains at rest or continues to move at a constant velocity, unless acted upon by a force. This law is quite "natural", especially when dealing with daily life activities relative to our "stationary" ground frame. Take for instance an Olympic ice dancer. While ice skating, she expects to keep her constant velocity if no obstacles are present. While going to sleep at night, she expects to stay in her bed...
That's when no forces are in action. What happens though, when an object is acted upon by a force? In this case the trajectory can be found by using Newton's second law.
But not all frames are Inertial. Relative to some frames, free objects follow an accelerated or a curved trajectory even though no forces are present. Observing the physical reality relative to such frames is counter intuitive. Take a look, for instance, at the excellent demonstration below. Not only is this strange but it also contradicts the law of inertia. A free body (not acted upon by forces) does not keep its constant velocity. In order to overcome this issue on the one hand while preserving Newton's laws on the other hand, sixteenth century physicists introduced the concept of fictitious forces. These forces were invented as the cause (i.e. the explanation) for the curved trajectories of free objects. However, the origin of these forces was unclear. It was not until Mach and Einstein that a more general understanding of the subject has emerged. In any case, fictitious forces are a necessary and a useful feature in classical mechanics. They are fictitious only in the sense that we cannot perceive their origin. In all other aspects they are real.
Let us sum up: a natural phenomenon can be described (by equations) relative to any frame of reference. In classical mechanics we are often interested in the trajectories of objects. While relative to Inertial frames the trajectory of a body can be found by using Newton's second law (which is reduced to constant-velocity motion when no forces are in action), the situation relative to non-Inertial frames is a bit different. Relative to non-Inertial frames Newton's second law can be used only when fictitious forces are added to the equation.
Motion in Non-Inertial Frames (Credit: udiprod)
The New Approach Explained
The new approach is actually a new model for the rotational velocities (i.e. a prediction). The core idea behind this prediction is the insight that the observed velocities might be given relative to a non-inertial frame. Relative to such a frame, as we already know, fictitious forces are in action. If those are to be taken into account within the model it might be possible to explain the gap. But before we dive more into details, let us start from the beginning. How do we measure the rotational velocities in galaxies?
The first step in our journey is observing a galaxy. Well... one may try it with his own naked eyes. But then, in order to meet current standards, one must: 1. have two radio-sensitive eyes, 2. be willing to stare at the same point for a very long time. Radio telescopes are just perfect for this mission. Therefore they are widely used for the extraction of rotation curves.
We are now ready for the second step: understanding the actual process of extracting the rotational velocities. However, this process is a broad field in astrophysics. The interested reader may find this link enlightening. Here we'll just mention the following:
1. The light emitted by a far object (e.g. some part of a galaxy) is detected in our telescope. Its spectral features are then extracted.
2. These features change their wavelength when an object is approaching or moving away (Doppler Effect). This allows astronomers to calculate the line-of-sight velocity of an object. In particular, the line-of-sight velocities of different parts in a given galaxy could be calculated.
3. Those line-of-sight velocities are then converted to rotational velocities through geometrical considerations.
Take a look, for example, at the observed rotational velocities of NGC 100 (the black error bars in the plot below).
The third step of our journey is fitting these observed values (e.g. the black error bars) with a model. We already understand that these values are valid only with respect to some specific frame of reference. Let's call this frame K'. Today, the majority of astrophysicists assume (implicitly most of the time) that K' is an Inertial frame. If indeed this is the case and K' is an Inertial frame, then Newton's laws can be used in their basic form (i.e. without fictitious forces). However, when these laws are used in their basic form in order to make a prediction (e.g. the blue curve), a discrepancy is revealed*. This Newtonian prediction takes into account the visible matter alone. Therefore, in order to resolve the discrepancy, a dark halo of non-baryonic matter is commonly added.
Our idea is to take a step back: what if the observed velocities (e.g. the black error bars) are not given with respect to the local inertial frame? In other words: what if K', the observational frame, is not Inertial? In that case, fictitious forces must be added to the Newtonian calculations. The "blue curve" will not be a valid prediction anymore. It might be possible to modify this prediction without invoking extra matter.
In our paper, we show that K' can be described as follows: a frame of reference whose fundamental plane (X'-Y') coincides with the plane of the observed galaxy and its fundamental axis (e.g. X') is directed toward the observer (see the illustration below). At first sight, it seems natural to assume that K' is an inertial frame. A distant earth-observer is static there (i.e. not rotating) and possibly all the far background is "fixed" there as well.
Question Number 1: Can K' be non-inertial?
Of course. If we are to follow our current understanding of physics, based on general relativity, the answer depends on the motion and distribution of the matter itself. Roughly speaking, when the background is fixed, our local frame is Inertial and no fictitious forces appear**. But we don't really know what the universe looks like from K'! We only know that the earth-observer is fixed there. The authors of this novel paper, for example, have found a coherence between galaxy rotation and the motion of its neighbors up to 12 Mpc. They found a signal (i.e. for a rotating background) that depends on the rotation of the galaxy itself. This (together with some other studies) suggests that we currently do not have sufficient information to decide whether K' is Inertial or not. In that case, the possible influence of fictitious forces must be taken into account as well in our models.
Question Number 2: What is the new prediction for the rotational velocities?
In our paper, we show that there is actually only one degree of freedom. We demonstrate that the local Inertial frame (from now on, K) must also contain a fundamental plane (X-Y) which coincides with the galactic plane. Therefore, the relative motion between the frames may contain only an angular velocity of one frame relative to the Z-axis of the other (see the illustration below). With this arrangement, the new prediction for the rotational velocities is simply the old prediction (e.g. the blue curve, which is now valid only relative to K) plus an w * r correction term. r is the distance from the center and w is the angular velocity of K relative to K'. This term simply represents the extra tangential velocity of an object relative to K'.***
Question Number 3: How fast does K rotate relative to K'? What is the value of w?
We don't know. We don't have enough information to decide a priori what the required transformation is. Therefore, in this work, w will be a free parameter. If, for example, w is equal to zero, then the observational frame is Inertial and we are back with the "blue prediction" again. However, if w gets another value, there might be a chance to fit the observed data with the predicted curve. Actually, a major part of our paper is devoted to searching the best-fit values of w (for a large number of galaxies). There are two important points to be mentioned in this context:
1. Using a free parameter, obviously, does not assure a good fit (or any fit) to the data. 2. Common dark halo profiles consist of two or three free parameters.
_______________________________________________________________________________
* To find out more about the discrepancy in galaxy rotation curves, please visit this page of the website.
** There might be other effects as well. An excellent review can be found here. In any case, this is a bit analogous to our situation on earth: when we look up and see the fixed stars, we don't feel anything special. However, when we sit on a carousel and the skies are swirling, we suddenly feel the fictitious forces all around us. These forces exist only relative to the carousel frame.
*** For the direction and magnitude of the fictitious forces (which are actually not necessary for the fitting process) please download our paper. These forces should be equal to the gravitational forces produced by a dark halo.
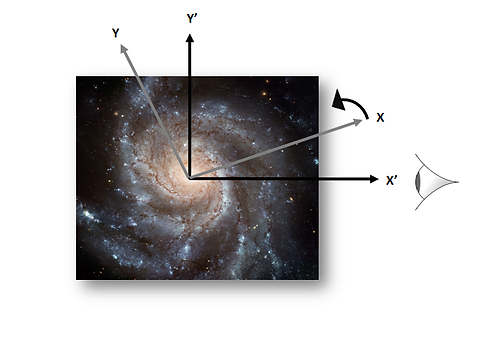
Frames of Reference
The measured velocities presented in RC's are valid only with respect to K' by definition. If K' is not Inertial, then the relative motion between K (the inertial frame) and K' (the observational frame) includes only rotation. The relation between the rotational velocities in the two frames is given by: Vk'(r) = Vk(r) + w * r
Results
In the previous section we introduced a possible explanation for the discrepancy. The bottom line can be described as follows: the new model for the rotational velocities V(r) should include an extra term (namely w * r). This extra term arises in non-inertial systems. It represents the additional tangential velocity relative to those systems. The motivation for using such a term comes from the simple insight that the observed velocities might actually be non-inertial.
In the following graphs we introduce the fittings of several different rotation curves. More details on the fitting process and the sample of galaxies can be found in the paper. Note that when plotting a graph such as a rotation curve (i.e. something vs radius), an w * r term is simply represented by straight line.
NGC 300
In this fit a value of w = 1.55 [10^-16 rad/sec] and a value of M/L = 0.97 [Msun/Lsun] were obtained.
___________________________________
The blue curve represents the prediction relative to a local Inertial frame (based on the visible matter alone). The green line is the extra term required in non-inertial frames and the red curve is our model's prediction.
Looking at the plots, the reader who is unfamiliar with this field of research may wonder whether these curves could be considered as good matches to the data? We won't go through a comprehensive statistical comparison, but let us mention this: these curves (and the rest of the predictions in our sample) can be regarded as very good matches to the observed data, as in most cases they achieve the same or better results than dark halos do, with fewer free parameters.
In fact, every astrophysicist who truly supports the dark halos view must wonder how a simple coordinates transformation can mimic so easily the behavior of those halos. If they are real, then an explanation for this coincidence should be found within the dark halos theory. In our paper, in any case, we show that the contribution of some known dark halo profiles (e.g. NFW, Burkert) is suspiciously similar to the effective contribution of fictitious force.
Another nice outcome is the consistency of our fits with Renzo’s experimental law. This law states that every time there is a feature in the radial light distribution, the observed rotation curve shows a corresponding feature. In our plots, the inertial contribution (e.g. our dear blue curve) is directly derived from the light (and gas) distributions. Indeed, adding only a straight line to to the blue curve would preserve every bump and every feature. A nice example is NGC 1560. This is not a good fit, but it can clearly be seen that the small "bump" in the data (at 5 Kpc) has a corresponding "bump" in the predicted curve. This is a natural and a strong result of our theory.
The dark halos theory, on the other hand, does not provide a satisfactory explanation to Renzo's findings. Assuming the dark halo is dominant (as it must be in the inner regions of LSBs for example), how come a small change in the baryonic distribution affects the rotational velocities significantly? There are several different explanations for this problem, of course. But they are very unsatisfactory by their nature. We argue that this kind of post-priori explanations might harm the long term progress of science.
The most significant result, from our perspective, is the sign of w. In order to fit the data, only positive w's are possible. This means that the local inertial frame K, is rotating relative to K', in the same direction as the direction of the revolving matter (for the exact details and definitions please see the paper). Why is this so? Is it dragged by the background? Is there any way to pre-define the local inertial frame?
Those are open questions that are waiting to be solved. Moreover, the method developed in our work is applicable only in flat galaxies. Is it possible to use the same insight in order to develop similar methods for other domains such as elliptical galaxies or galaxy clusters? The discrepancies in those domains are no less important than the one in galaxy rotation curves.
Therefore, we hereby declare on the Century's Competition! We offer a 3.1415 $ prize to the first person to give a satisfactory answer to one of the questions above. The prize will be collected from the International Institute of Pure Science. On a slightly more serious note, we express our deepest hope that the idea we present here will lead to a broader look of the current problems in astrophysics and inspire future scientists.
